Furtwängler Philipp Friedrich Pius, Mathematiker. Geb. Elze, Preußen (D), 21. 4. 1869; gest. Wien, 19. 5. 1940; evang. AB. Enkel des Orgelbauers Philipp Furtwängler (1800–1867), Sohn des Orgelbauers Wilhelm Furtwängler (1829–1883) und von dessen Gattin Mathilde Furtwängler, geb. Sander; in erster Ehe mit Ella Furtwängler, geb. Buchwald, ab 1929 mit Emilie Furtwängler, geb. Schön, verheiratet. – Nach Besuch des Gymnasiums Andreanum in Hildesheim studierte F. 1889–94 Mathematik, Physik sowie Chemie an der Universität Göttingen. 1894–95 wirkte er als Assistent am Physikalischen Institut der TH Darmstadt und legte daneben in Göttingen die Lehramtsprüfung aus Mathematik, Physik, Chemie und Mineralogie ab; 1895 Dr. phil., vertiefte er bis 1896 seine Ausbildung an der dortigen Universität. Nach dem Einjährig-Freiwilligen-Jahr absolvierte er zwei Probejahre an Mittelschulen in Hannover, Norden und Celle zum Erwerb der Befähigung als Oberlehrer. 1898–1904 arbeitete F. zunächst als Assistent, dann als wissenschaftliche Hilfskraft am Geodätischen Institut in Potsdam, wo er gemeinsam mit Friedrich Kühnen absolute Schwerkraftmessungen durchführte. Darüber hinaus nahm er Schwerkraftmessungen in Schlesien und im Harz sowie Präzisionsnivellements an der Ostseeküste zur Kontrolle der dortigen Pegel vor. Ohne sich je habilitiert zu haben, hielt er ab 1904 Vorlesungen für Landvermesser an der Preußischen landwirtschaftlichen Akademie in (Bonn-)Poppelsdorf, ab 1907 wirkte er als Professor für Mathematik an der TH in Aachen, ab 1910 als Professor für Mathematik wieder an der Preußischen landwirtschaftlichen Akademie in (Bonn-)Poppelsdorf und hatte zugleich einen Lehrauftrag für angewandte Mathematik an der Universität Bonn. 1912 erhielt er einen Ruf als o. Prof. für Mathematik an die Universität Wien. Hier wurde er auch Mitglied der Prüfungskommission für das Lehramt an Mittelschulen. Ab 1937/38 konnte er aus gesundheitlichen Gründen keine Vorlesungen mehr halten, im September 1938 trat er endgültig in den Ruhestand. F. lieferte zunächst Beiträge zur angewandten Mathematik und höheren Geodäsie und entwickelte sich dann zu einem bedeutenden Zahlentheoretiker. Sein Interesse galt aber auch der höheren Algebra. In Potsdam beschäftigte er sich vor allem mit Problemen zur Bestimmung der absoluten Schwerkraft, was ihn zum Redakteur des 6. Bandes „Geodäsie und Geophysik“ (1906–25) der „Enzyklopädie der Mathematischen Wissenschaften“ qualifizierte. Zwei von David Hilpert formulierte mathematische Probleme ließen ihn durch 30 Jahre nicht los: der Beweis der Reziprozitätsgesetze in algebraischen Zahlkörpern und jener der Existenz von Klassenkörpern. Schließlich wurde er mit dem allgemeinen Beweis des Hauptidealsatzes (1928) berühmt, wobei er auf Vorarbeiten von Emil Artin zurückgreifen konnte. Zusätzlich stellte er das sogenannte Furtwängler’sche Kriterium zum Fermat’schen Satz auf und lieferte Beiträge zu der von Hermann Minkowski begründeten Geometrie der Zahlen, aus deren Bereich auch seine Dissertation stammte. Darüber hinaus beschäftigte er sich mit der Technik des damals populär gewordenen Radios. F. war ab 1916 korrespondierendes, ab 1927 wirkliches Mitglied der (kaiserlichen) Akademie der Wissenschaften in Wien, ab 1931 korrespondierendes Mitglied der Preußischen Akademie der Wissenschaften in Berlin, ab 1939 Mitglied der Deutschen Akademie der Naturforscher Leopoldina sowie Mitglied der Deutschen Mathematiker-Vereinigung. 1901 erhielt er für seine zahlentheoretischen Arbeiten den Preis der Königlichen Gesellschaft der Wissenschaften in Göttingen, 1930 die Ernst-Abbé-Gedächtnismedaille. Der 48. Band der „Monatshefte für Mathematik und Physik“ (1939) wurde ihm zum 70. Geburtstag gewidmet.
L.: NDB; Poggendorff 5–7a (m. W.); W. Lorey, in: Zeitschrift für Angewandte Mathematik und Mechanik 19, 1939, S. 191f.; E. Cermak, Beiträge zur Geschichte des Lehrkörpers der Philosophischen Fakultät der Universität Wien zwischen 1938 und 1945, phil. Diss. Wien, 1980, S. 74f.; K. Körrer, Die zwischen 1938 und 1945 verstorbenen Mitglieder des Lehrkörpers an der Universität Wien, phil. Diss. Wien, 1981, S. 53f.; R. Einhorn, Vertreter der Mathematik und Geometrie an den Wiener Hochschulen 1900–1940, 1, 1985, S. 96–111 (m. W.), 2, Taf. IV (B.); D. D. Fenster – J. Schwermer, Beyond Class Field Theory …, in: Archive for History of Exact Sciences 61, 2007, S. 432, 441, 445f., 454; Briefwechsel H. Hasse – P. F., ed. P. J. Roquette, 2007 (nur online); M. Hörlesberger, Zur Rezeption der Modernen Algebra in Österreich, 2008, passim; C. Zong, Geometry of Numbers in Vienna, in: The Mathematical Intelligencer 31, 2009, S. 25–31 (m. B.); A. Čap u. a., Mathematik in Wien …, in: Internationale Mathematische Nachrichten 64, 2010, Nr. 214, S. 2–4; Archiv der Österreichischen Akademie der Wissenschaften, UA, WStLA, alle Wien; Rheinisch-Westfälische TH, Aachen, D.
 )
) 
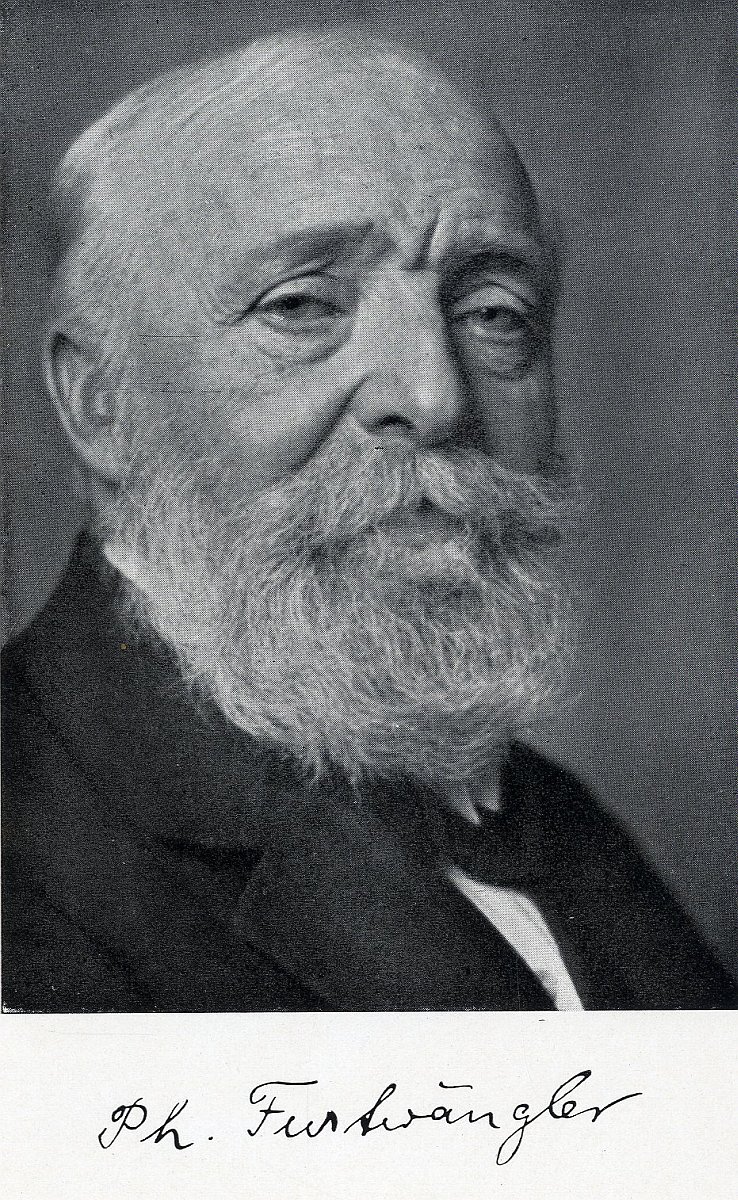 Porträt
Porträt Porträt
Porträt